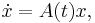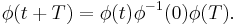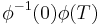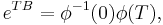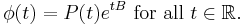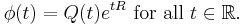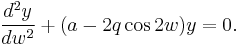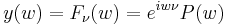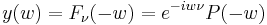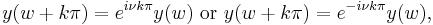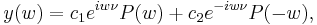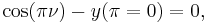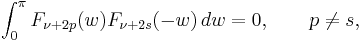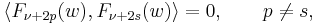Floquet theory
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to linear differential equations of the form
with 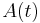 a piecewise continuous periodic function with period
a piecewise continuous periodic function with period  .
.
The main theorem of Floquet theory, Floquet's theorem, due to Gaston Floquet (1883), gives a canonical form for each fundamental matrix solution of this common linear system. It gives a coordinate change 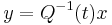 with
with 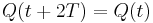 that transforms the periodic system to a traditional linear system with constant, real coefficients.
that transforms the periodic system to a traditional linear system with constant, real coefficients.
In solid-state physics, the analogous result (generalized to three dimensions) is known as Bloch's theorem.
Note that the solutions of the linear differential equation form a vector space. A matrix 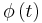 is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix
is called a fundamental matrix solution if all columns are linearly independent solutions. A matrix 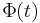 is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists
is called a principal fundamental matrix solution if all columns are linearly independent solutions and there exists 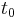 such that
such that 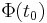 is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using
is the identity. A principal fundamental matrix can be constructed from a fundamental matrix using 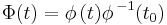 . The solution of the linear differential equation with the initial condition
. The solution of the linear differential equation with the initial condition 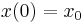 is
is 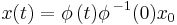 where
where 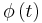 is any fundamental matrix solution.
is any fundamental matrix solution.
Contents |
Floquet's theorem
Let 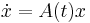 be a linear first order differential equation, where
be a linear first order differential equation, where 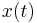 is a column vector of length
is a column vector of length  and
and 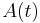 an
an 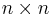 periodic matrix with period
periodic matrix with period  (that is
(that is 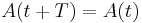 for all real values of
for all real values of  ). Let
). Let 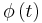 be a fundamental matrix solution of this differential equation. Then, for all
be a fundamental matrix solution of this differential equation. Then, for all 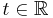 ,
,
Here
is known as the monodromy matrix. In addition, for each matrix  (possibly complex) such that
(possibly complex) such that
there is a periodic (period  ) matrix function
) matrix function 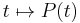 such that
such that
Also, there is a real matrix  and a real periodic (period-
and a real periodic (period-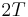 ) matrix function
) matrix function 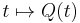 such that
such that
In the above  ,
,  ,
,  and
and  are
are 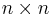 matrices.
matrices.
Consequences and applications
This mapping 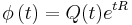 gives rise to a time-dependent change of coordinates (
gives rise to a time-dependent change of coordinates (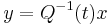 ), under which our original system becomes a linear system with real constant coefficients
), under which our original system becomes a linear system with real constant coefficients 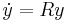 . Since
. Since 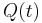 is continuous and periodic it must be bounded. Thus the stability of the zero solution for
is continuous and periodic it must be bounded. Thus the stability of the zero solution for 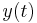 and
and 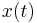 is determined by the eigenvalues of
is determined by the eigenvalues of  .
.
The representation 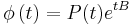 is called a Floquet normal form for the fundamental matrix
is called a Floquet normal form for the fundamental matrix 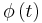 .
.
The eigenvalues of 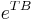 are called the characteristic multipliers of the system. They are also the eigenvalues of the (linear) Poincaré maps
are called the characteristic multipliers of the system. They are also the eigenvalues of the (linear) Poincaré maps 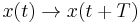 . A Floquet exponent (sometimes called a characteristic exponent), is a complex
. A Floquet exponent (sometimes called a characteristic exponent), is a complex  such that
such that 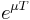 is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since
is a characteristic multiplier of the system. Notice that Floquet exponents are not unique, since 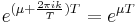 , where
, where  is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stable if the Lyapunov exponents are nonpositive and unstable otherwise.
is an integer. The real parts of the Floquet exponents are called Lyapunov exponents. The zero solution is asymptotically stable if all Lyapunov exponents are negative, Lyapunov stable if the Lyapunov exponents are nonpositive and unstable otherwise.
- Floquet theory is very important for the study of dynamical systems.
- Floquet theory shows stability in Hill differential equation (introduced by George William Hill) approximating the motion of the moon as a harmonic oscillator in a periodic gravitational field.
Floquet's theorem applied to Mathieu equation
Mathieu's equation is related to the wave equation for the elliptic cylinder.
Given 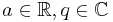 , the Mathieu equation is given by
, the Mathieu equation is given by
The Mathieu equation is a linear second-order differential equation with periodic coefficients.
One of the most powerful results of Mathieu's functions is the Floquet's Theorem [1, 2]. It states that periodic solutions of Mathieu equation for any pair (a, q) can be expressed in the form
or
where  is a constant depending on a and q and P(.) is
is a constant depending on a and q and P(.) is  -periodic in w.
-periodic in w.
The constant  is called the characteristic exponent.
is called the characteristic exponent.
If  is an integer, then
is an integer, then 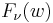 and
and 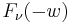 are linear dependent solutions. Furthermore,
are linear dependent solutions. Furthermore,
for the solution 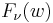 or
or 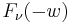 , respectively.
, respectively.
We assume that the pair (a, q) is such that 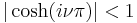 so that the solution
so that the solution 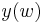 is bounded on the real axis. General solution of Mathieu's equation (
is bounded on the real axis. General solution of Mathieu's equation (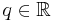 ,
,  non-integer) is the form
non-integer) is the form
where 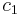 and
and 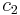 are arbitrary constants.
are arbitrary constants.
All bounded solutions --those of fractional as well as integral order-- are described by an infinite series of harmonic oscillations whose amplitudes decrease with increasing frequency.
Another very important property of Mathieu's functions is the orthogonality [3]:
If 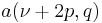 and
and 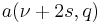 are simple roots of
are simple roots of
then:
i.e.,
where <.,.> denotes an inner product defined from 0 to π.
References
- C. Chicone. Ordinary Differential Equations with Applications. Springer-Verlag, New York 1999.
- Ekeland, Ivar (1990). "One". Convexity methods in Hamiltonian mechanics. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]. 19. Berlin: Springer-Verlag. pp. x+247. ISBN 3-540-50613-6. MR1051888.
- Floquet, Gaston (1883), "Sur les équations différentielles linéaires à coefficients périodiques", Ann. École Norm. Sup. 12: 47–88, http://archive.numdam.org/ARCHIVE/ASENS/ASENS_1883_2_12_/ASENS_1883_2_12__47_0/ASENS_1883_2_12__47_0.pdf
- Krasnosel'skii, M.A. (1968), The Operator of Translation along the Trajectories of Differential Equations, Providence: American Mathematical Society, Translation of Mathematical Monographs, 19, 294p.
- W. Magnus, S. Winkler. Hill's Equation, Dover-Phoenix Editions, ISBN 0-486-49565-5.
- N.W. McLachlan, Theory and Application of Mathieu Functions, New York: Dover, 1964.
- Teschl, Gerald. Ordinary Differential Equations and Dynamical Systems. Providence: American Mathematical Society. http://www.mat.univie.ac.at/~gerald/ftp/book-ode/.
- M.S.P. Eastham, "The Spectral Theory of Periodic Differential Equations", Texts in Mathematics, Scottish Academic Press, Edinburgh, 1973.